Charakteristiky kapilár a příklady ve vodě
kapilární Je to vlastnost kapalin, která jim umožňuje pohybovat se trubkovými otvory nebo porézními povrchy i proti gravitační síle. K tomu musí existovat rovnováha a koordinace dvou sil spojených s molekulami kapaliny: soudržnost a adheze; které mají tyto dva fyzikální odrazy nazývané povrchové napětí.
Tekutina musí být schopna zvlhčit vnitřní stěny trubky nebo póry materiálu, kterým se pohybuje. K tomu dochází, když je síla adheze (stěna kapilární kapiláry) větší než síla intermolekulární soudržnosti. V důsledku toho tvoří kapalné molekuly silnější interakce s atomy materiálu (sklo, papír atd.) Než mezi nimi.
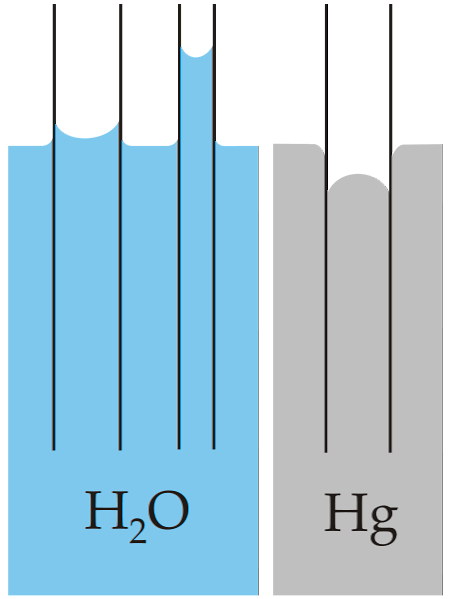
Klasický příklad kapilárnosti je ilustrován ve srovnání této vlastnosti pro dvě velmi odlišné kapaliny: vodu a rtuť.
Horní obrázek ukazuje, že voda stoupá skrz stěny trubky, což znamená, že má vyšší adhezní síly; zatímco opak se stane s rtutí, protože jeho soudržné, kovové spojovací síly zabrání smáčení skla.
Z tohoto důvodu voda tvoří konkávní meniskus a rtuť je konvexní meniskus (kopulovitý). Je třeba také poznamenat, že čím menší je poloměr trubky nebo úsek, kterým se kapalina pohybuje, tím větší je ujetá výška nebo vzdálenost (porovnejte výšky vodních sloupců pro obě trubky)..
Index
- 1 Charakteristika kapilárnosti
- 1.1 - Povrch kapaliny
- 1.2 -Hight
- 1.3 - Povrchové napětí
- 1.4 -Radio kapiláry nebo póry, kde kapalina stoupá
- 1,5 - Úhel kontaktu (θ)
- 2 Kapilárnost vody
- 2.1 Na rostlinách
- 3 Odkazy
Charakteristiky kapilár
-Povrch kapaliny
Povrch kapaliny, například vody, v kapiláře je konkávní; to znamená, že meniskus je konkávní. K této situaci dochází proto, že výsledkem sil vyvíjených na molekuly vody v blízkosti stěny trubice je směr.
Ve všech meniskách je kontaktní úhel (θ), což je úhel, který tvoří stěnu kapilární trubice s přímkou tečnou k povrchu kapaliny v místě kontaktu.
Přilnavost a soudržnost
Jestliže síla adheze kapaliny k kapilární stěně převažuje nad mezimolekulovou soudržností, pak úhel je < 90º; el líquido moja la pared capilar y el agua asciende por el capilar, observándose el fenómeno conocido como capilaridad.
Když se na povrch čistého skla umístí kapka vody, na sklenici se rozšíří voda, takže θ = 0 a cos θ = 1.
Pokud intermolekulární kohezní síla převažuje nad pevností kapiláry, např. V rtuti, kapalinovou stěnou, bude meniskus konvexní a úhel θ bude mít hodnotu> 90 °; rtuť nezvlhčuje kapilární stěnu, a proto sestupuje vnitřní stěnou.
Když je kapka rtuti umístěna na povrch čistého skla, kapka si zachovává svůj tvar a úhel θ = 140º.
-Výška
Voda stoupá kapilární trubkou, aby dosáhla výšky (h), ve které hmotnost vodního sloupce kompenzuje vertikální složku intermolekulární kohezní síly.
Jak stoupá více vody, dojde k bodu, kdy gravitace zastaví jeho vzestup, i když povrchové napětí působí ve váš prospěch.
Když se to stane, molekuly nemohou dále „stoupat“ po vnitřních stěnách a všechny fyzické síly jsou vyrovnávány. Na jedné straně máte síly, které podporují vzestup vody, a na druhé straně vaše vlastní váha tlačí dolů.
Jurinův zákon
To lze psát matematicky následovně:
2 π rΥcosθ = ρgπr2h
Kde levá strana rovnice závisí na povrchovém napětí, jehož velikost také souvisí s kohezními nebo intermolekulárními silami; Cos0 představuje kontaktní úhel a r poloměr díry, kterou kapalina stoupá.
Na pravé straně rovnice máme výšku h, gravitační sílu g a hustotu kapaliny; to by byla voda.
Vymazání pak máte
h = (2Υcosθ / ρgr)
Tato formulace je známa jako Jurinův zákon, který definuje výšku dosaženou kapalinovým sloupcem, v kapilární trubici, když je hmotnost kapalného sloupce vyvážena silou vzestupu kapilárností..
-Povrchové napětí
Voda je dipolární molekula, kvůli electronegativity atomu kyslíku a jeho molekulární geometrii. Toto způsobí, že část molekuly vody kde kyslík je lokalizován být záporně nabitý, zatímco část molekuly vody, obsahovat 2 atomy vodíku, je kladně nabitý \ t.
Molekuly v kapalině díky tomu prostřednictvím několika vodíkových vazeb vzájemně ovlivňují. Molekuly vody, které jsou v rozhraní voda: vzduch (povrch), však podléhají čisté přitažlivosti molekulami kapalného sinusu, které nejsou kompenzovány slabou přitažlivostí molekulami vzduchu..
Molekuly vody rozhraní jsou proto vystaveny přitažlivé síle, která má tendenci odstraňovat molekuly vody z rozhraní; to znamená, že vodíkové můstky vytvořené s molekulami ve dně táhnou ty, které jsou na povrchu. Povrchové napětí se tedy snaží zmenšit povrch rozhraní voda: vzduch.
Vztah s h
Když se podíváte na rovnici Jurinova zákona, zjistíte, že h je přímo úměrné Υ; proto čím větší je povrchové napětí kapaliny, tím větší je výška, která může stoupat kapilárou nebo pórem materiálu.
Lze tedy očekávat, že u dvou kapalin, A a B, s různým povrchovým napětím, vzroste ten s nejvyšším povrchovým napětím na vyšší výšku.
Z tohoto bodu lze vyvodit, že nejdůležitější vlastností, která definuje kapilární vlastnost kapaliny, je vysoké povrchové napětí.
-Poloměr kapiláry nebo póru, kde kapalina stoupá
Pozorování zákona Jurina naznačuje, že výška dosažená kapalinou v kapiláře nebo póru je nepřímo úměrná poloměru stejné.
Čím menší je tedy poloměr, tím větší je výška, kterou kapalinový sloupec dosáhne kapilárním působením. To lze vidět přímo na obrázku, kde se voda porovnává s rtutí.
Ve skleněné trubici o poloměru 0,05 mm dosáhne vodní sloupec kapilární výškou 30 cm. V kapilárních trubicích s poloměrem 1 μm se sacím tlakem 1,5 x 103 hPa (což se rovná 1,5 atm) odpovídá výpočtu výšky vodního sloupce od 14 do 15 m.
To je velmi podobné tomu, co se děje s těmi brčka, která se několikrát točí. Sáním kapaliny vzniká tlakový rozdíl, který způsobuje, že kapalina stoupá do úst.
Maximální hodnota výšky sloupce dosaženého kapilárou je teoretická, protože poloměr kapilár nelze snížit nad určitou hranici.
Zákon Poiseuille
Z toho vyplývá, že tok skutečné kapaliny je dán následujícím výrazem:
Q = (πr4/ 8ηl) AP
Kde Q je průtok kapaliny, η je jeho viskozita, 1 délka trubky a ΔP tlakový rozdíl.
Při snižování poloměru kapiláry by se měla výška sloupce kapaliny dosahovaná kapilárou zvyšovat na dobu neurčitou. Nicméně, Poiseuille poukazuje na to, že zmenšení poloměru také snižuje tok kapaliny touto kapilárou.
Kromě toho by viskozita, která je měřítkem odporu, který je proti proudu skutečné kapaliny, dále snižovala tok kapaliny.
-Úhel kontaktu (θ)
Čím vyšší je hodnota cosθ, tím vyšší je výška vodního sloupce kapilárností, jak naznačuje Jurinův zákon.
Jestliže θ je malé a blíží se nule (0), cosθ je = 1, takže hodnota h bude maximální. Naopak, jestliže θ je rovno 90 °, cosθ = 0 a hodnota h = 0.
Když je hodnota θ větší než 90 °, což je případ konvexního menisku, kapalina nevzrůstá kapilárou a její tendence je klesat (jak je tomu u rtuti).
Vodní kapilárnost
Voda má hodnotu povrchového napětí 72,75 N / m, relativně vysokou ve srovnání s hodnotami povrchového napětí následujících kapalin:
-Aceton: 22,75 N / m
-Ethylalkohol: 22,75 N / m
-Hexan: 18,43 N / m
-Methanol: 22,61 N / m.
Voda má proto výjimečné povrchové napětí, což podporuje rozvoj kapilárního jevu, který je nezbytný pro absorpci vody a živin rostlinami..
Na rostlinách

Kapilárnost je důležitým mechanismem pro vzestup mízy xylémem rostlin, ale samo o sobě nestačí, aby míza dosáhla listů stromů..
Transpirace nebo odpařování je důležitým mechanismem ve výstupu mízy xylémem rostlin. Listy ztrácejí vodu odpařováním, což vede ke snížení množství molekul vody, což způsobuje přitažlivost molekul vody přítomných v kapilárních trubicích (xylem).
Molekuly vody nepůsobí nezávisle na sobě, ale interagují Van der Waalsovými silami, což je způsobuje, že stoupají spojeny kapilárními trubkami rostlin směrem k listům..
Kromě těchto mechanismů je třeba poznamenat, že rostliny absorbují vodu z půdy osmózou a že pozitivní tlak vytvářený v kořenech pohání začátek výstupu vody přes kapiláry rostliny..
Odkazy
- García Franco A. (2010). Povrchní jevy. Zdroj: sc.ehu.es
- Povrchové jevy: povrchové napětí a kapilárnost. [PDF] Zdroj: ugr.es
- Wikipedia. (2018). Capillarity Zdroj: en.wikipedia.org
- Risvhan T. (s.f.) Kapilárnost v rostlinách. Zdroj: academia.edu
- Helmenstine, Anne Marie, Ph.D. (22. prosince 2018). Kapilární akce: Definice a příklady. Citováno z: thoughtco.com
- Ellen Ellis M. (2018). Kapilární působení vody: Definice a příklady. Studie. Zdroj: study.com
- Personál ScienceStruck. (16. července 2017). Příklady, které vysvětlují koncept a význam kapilární akce. Citováno z: sciencestruck.com


