Kolik hran má hexagonální hranol?
Chcete vědět kolik hran má hexagonální hranol význam "hrany", "hranolu" a "šestiúhelníku" musí být znám. První dva pojmy jsou obecné definice a třetí pojem souvisí s tvarem geometrického útvaru.
Když mluvíme o šestiúhelníku, zmínka je tvořena šestiúhelníkem (mnohoúhelník). Předpona "hexa" označuje, že mnohoúhelník má šest stran.

Okraj je hranou objektu. Geometricky se jedná o čáru, která spojuje dva po sobě následující vrcholy geometrického útvaru.
Hranol je geometrický obrazec omezený dvěma základy, které jsou paralelní a rovné polygony a jejich boční strany jsou rovnoběžníky.
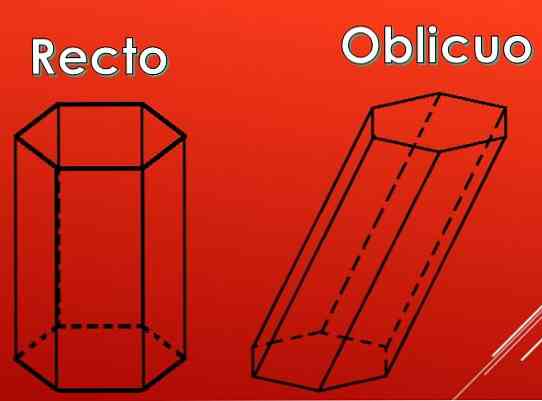
V následujícím obrázku je vidět, že boční plochy hexagonálního hranolu mohou být obdélníky, ale mohou být také rovnoběžníky.
Podle typu paralelogramů lze pojistné rozdělit do dvou typů: rovné a šikmé.
Jak spočítat hrany hexagonálního hranolu?
Počet hran, které bude mít hexagonální hranol, se nezmění, pokud se jedná o rovný nebo šikmý hranol. Počet hran také nezávisí na délce stran.
Počítání hran šestihranného hranolu může být provedeno několika způsoby. Zde jsou dva způsoby:
1. Rozložte hranol
Jeden způsob, jak spočítat hrany, je rozložením hexagonálního hranolu v jeho dvou základnách a jeho bočních plochách. Tímto způsobem získáte dva šestiúhelníky a rovnoběžník s pěti vnitřními liniemi.
Každý šestiúhelník má šest hran, proto hranol bude mít více než 12 hran.
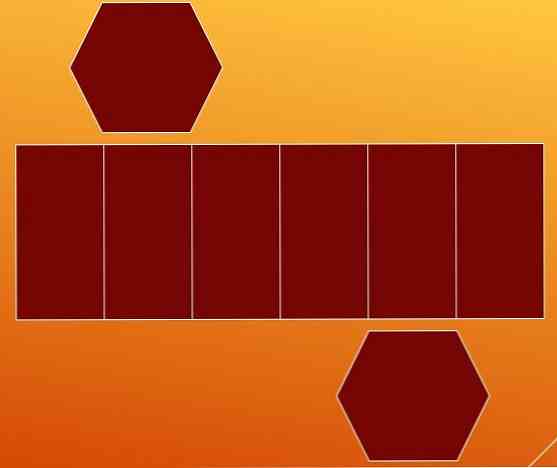
Na první pohled se předpokládá, že rovnoběžník obsahuje devět hran (sedm svislých a dvě vodorovné). Ale je vhodné zastavit analýzu tohoto případu.
Když je rovnoběžník ohnutý, aby vytvořil hranol, je vidět, že první řádek vlevo se spojí s posledním řádkem vpravo, s nímž obě čáry představují jeden okraj..
Ale co ty dvě vodorovné čáry?
Když jsou všechny kusy znovu spojeny, vodorovné čáry budou spojeny, každá se šesti hranami každého šestiúhelníku. Z tohoto důvodu by bylo jejich počítání zvlášť chybné.
Paralelogram tedy obsahuje šest hran hranolu, které spolu s 12 hranami počítanými na začátku dává celkem 18 hran.
2.- Promítání každé hrany
Jiným způsobem, mnohem jednodušší spočítat hrany, je skutečnost, že základny šestihranných hranolů jsou šestiúhelníky, pak každá základna má šest hran..
Na druhé straně, od každého vrcholu hexagon, jeden okraj je promítán k odpovídajícímu vrcholu druhého šestiúhelníku; to znamená, že existuje šest hran, které spojují jednu základnu s druhou.
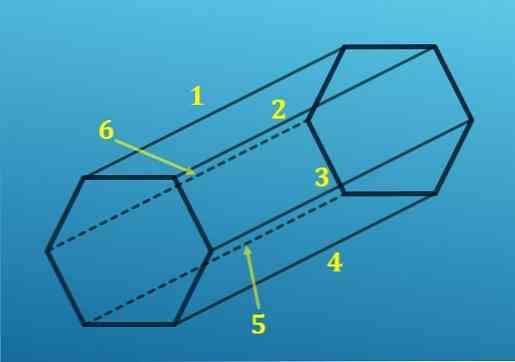
Přidáním všech hran získáte celkem 18 hran.
Závěr
Je možné ukázat, že počet hran hranolu se rovná trojnásobku počtu hran, které polygon tvoří, což má.
Pětiúhelníkový hranol tedy bude mít 3 * 5 = 15 hran, hepatogonální hranol bude mít 3 * 7 = 21 hran a může být tedy aplikován na jakýkoliv hranol.
Odkazy
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: přístup k řešení problémů učitelů základních škol. López Mateos Editori.
- Fregoso, R. S., & Carrera, S. A. (2005). Matematika 3. Editorial Progreso.
- Gallardo, G., & Pilar, P. M. (2005). Matematika 6. Editorial Progreso.
- Gutiérrez, C. T., & Cisneros, M. P. (2005). 3. Matematický kurz. Editorial Progreso.
- Kinsey, L., & Moore, T. E. (2006). Symetrie, tvar a prostor: Úvod do matematiky přes geometrii (ilustrovaný, dotisk ed.). Springer Science & Business Media.
- Mitchell, C. (1999). Oslňující Matematika Line vzory (Ilustrovaná ed.). Scholastic Inc.
- R., M. P. (2005). Kreslím 6º. Editorial Progreso.


