Vzorce úhlového posunutí a řešená cvičení
úhlové posunutí je generován, když se objekt pohybuje po cestě nebo cestě, která má tvar kruhu. Odlišuje se od posunutí; zatímco úhlové posunutí měří úhel, který se pohybuje, posunutí měří vzdálenost.
Pro výpočet úhlového posunutí objektu, který se pohybuje po obvodu, lze použít dva způsoby: pokud je znám počáteční a konečný úhel, pak úhlové posunutí bude odčítáním mezi konečným úhlem a počátečním úhlem.
Pokud je známa délka posunutí (délka obloukového oblouku) a poloměr obvodu, pak je úhlové posunutí dáno θ = l / r.
Index
- 1 Vzorce
- 2 Cvičení
- 2.1 První cvičení
- 2.2 Druhé cvičení
- 2.3 Třetí cvičení
- 3 Odkazy
Vzorce
Pro získání výše popsaných vzorců můžete vidět následující obrázky:
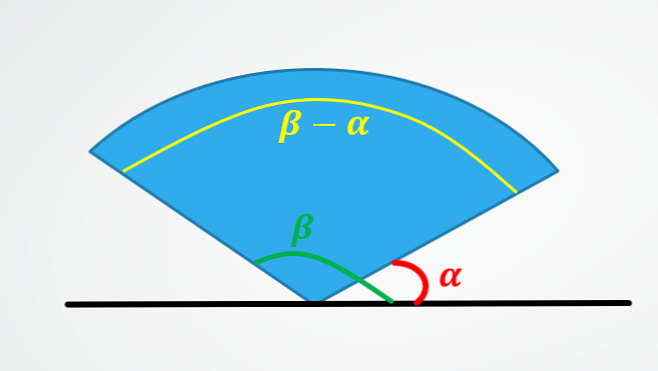
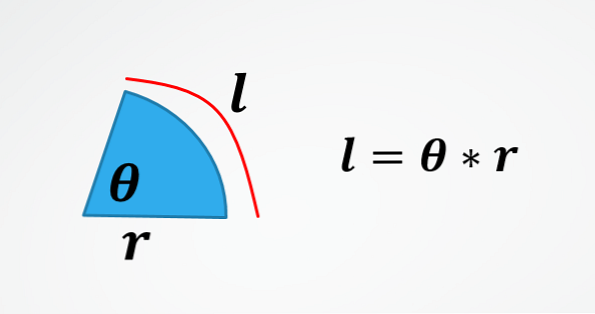
První z nich ukazuje, proč se úhlové posunutí rovná odečtení konečného úhlu mínus počáteční úhel.
Ve druhém obrázku je vzorec pro délku oblouku kruhu. Vymazáním θ získáte vzorec popsaný na začátku.
Cvičení
Níže jsou uvedena některá cvičení, kde by měla být použita definice úhlového posunutí a kde jsou použity výše popsané vzorce.
První cvičení
Na kruhové běžecké dráze, jejíž poloměr je roven 7 metrům, je Juan vzdálený 35 metrů. Vypočtěte úhlový posun, který provedl Juan.
Řešení
Vzhledem k tomu, že je známa vzdálenost mezi obloukem a poloměrem obvodu, lze použít druhý vzorec, aby bylo známo úhlové posunutí provedené Juanem. Pomocí výše uvedeného vzorce máte, že θ = 35/7 = 5 radiánů.
Druhé cvičení
Máte-li, že Mario cestoval v polovině své kruhové závodní dráhy, jaký je úhlový posun, který udělal Mario??
Řešení
V tomto cvičení bude aplikován první vzorec. Vzhledem k tomu, že je známo, že Mario cestoval polovinou trati, lze předpokládat, že startoval závod v úhlu 0 ° a když se dostal do středu kruhu, prošel 180 °. Odpověď je tedy 180 ° -0 ° = 180 ° = π radiánů.
Třetí cvičení
María má kruhový bazén. Váš pes pobíhá kolem bazénu o délce 18 metrů. Pokud je poloměr bazénu 3 metry, jaký je úhlový posun Mariiným maskotem??
Řešení
Vzhledem k tomu, že fond je kruhový a znáte jeho poloměr, můžete použít druhý vzorec.
Je známo, že poloměr je roven 3 metry a vzdálenost ujetá zvířetem je 18 metrů. Proto je provedené úhlové posunutí rovné θ = 18/3 = 6 radiánů.
Odkazy
- Basto, J. R. (2014). Matematika 3: Základní analytická geometrie. Redakční skupina Patria.
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: přístup k řešení problémů učitelů základních škol. López Mateos Editori.
- Bult, B., & Hobbs, D. (2001). Matematický slovník (znázorněno na obr.). (F. P. Cadena, Trad.) Edice AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Matematika Geometrie Reforma horního cyklu E.G.B. Ministerstvo školství.
- Schneider, W., & Sappert, D. (1990). Praktický technický nákres: úvod do základů průmyslového technického kreslení. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Výpočet: několik proměnných. Pearson Education.


