Kolik os Symetrie má kruh?
osy symetrie kruhu Jsou nekonečné. Tyto osy jsou ty, které rozdělují geometrický tvar do dvou přesně stejných polovin.
Kruh se skládá ze všech bodů, jejichž vzdálenost k pevnému bodu je menší nebo rovna určité hodnotě "r"..
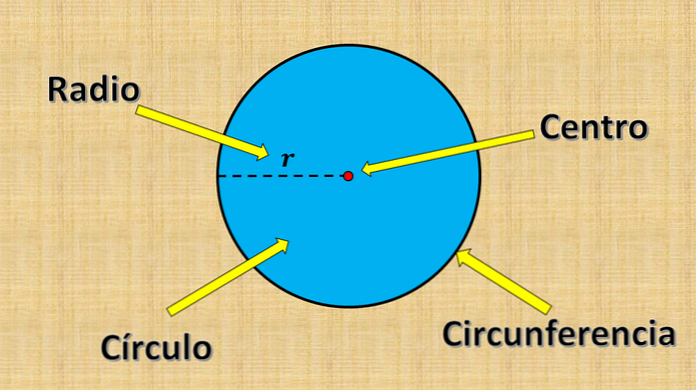
Výše uvedený pevný bod se nazývá střed a hodnota "r" se nazývá poloměr. Poloměr je největší vzdálenost mezi bodem na kruhu a středem.
Na druhé straně, jakýkoliv úseček, jehož konce jsou na okraji kruhu (obvod) a prochází středem, se nazývá průměr. Jeho měření je vždy rovno dvojnásobku poloměru.
Kruh a obvod
Nezaměňujte kruh s kruhem. Obvod se vztahuje pouze na body, které jsou ve vzdálenosti „r“ od středu; to znamená pouze okraj kruhu.
Při pohledu na osy symetrie je však lhostejné, pokud pracujete s kruhem nebo s kruhem.
Co je osa symetrie?
Osa symetrie je čára, která se dělí na dvě stejné části na určitý geometrický obrazec. Jinými slovy, osa symetrie se chová jako zrcadlo.
Šachty symetrie kruhu
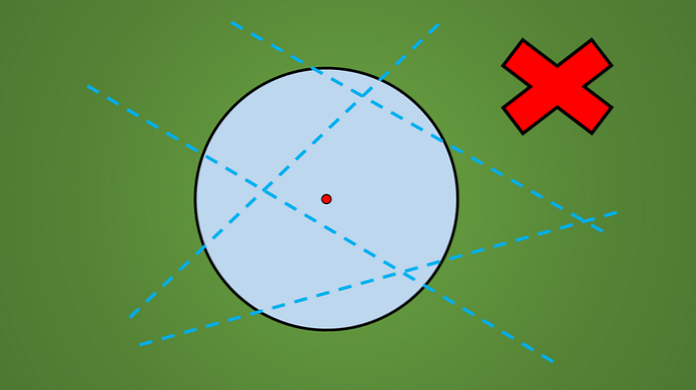
Pokud pozorujete jakýkoliv kruh, bez ohledu na jeho poloměr, můžete vidět, že ne každý řádek, který prochází, je osou symetrie.
Například žádná z čar nakreslených v následujícím obrázku není osou symetrie.
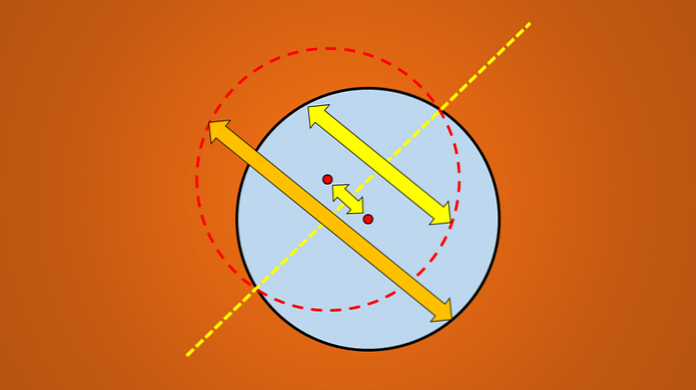
Snadný způsob, jak zkontrolovat, zda čára je osa symetrie nebo ne, je odrážet kolmo geometrický obrazec na opačnou stranu čáry.
Pokud odraz neodpovídá původnímu obrázku, pak tato čára není osou symetrie. Následující obrázek ilustruje tuto techniku.
Je-li však uvažován následující obraz, je dobře známo, že nakreslená čára je osou symetrie kruhu.
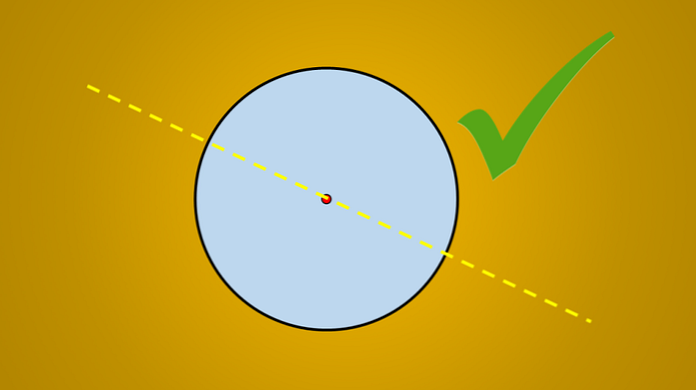
Otázkou je, zda existuje více os symetrie? Odpověď zní ano. Pokud tuto čáru otočíte o 45 ° proti směru hodinových ručiček, získaná linie je také osou symetrie kruhu.
Totéž platí, pokud otočíte o 90 °, 30 °, 8 ° a obecně o libovolný počet stupňů.
Důležité na těchto řádcích není sklon, který mají, ale všichni jdou přes střed kruhu. Proto jakákoliv čára, která obsahuje průměr kruhu, je osou symetrie.
Protože kruh má nekonečný počet průměrů, pak má nekonečný počet os symetrie..
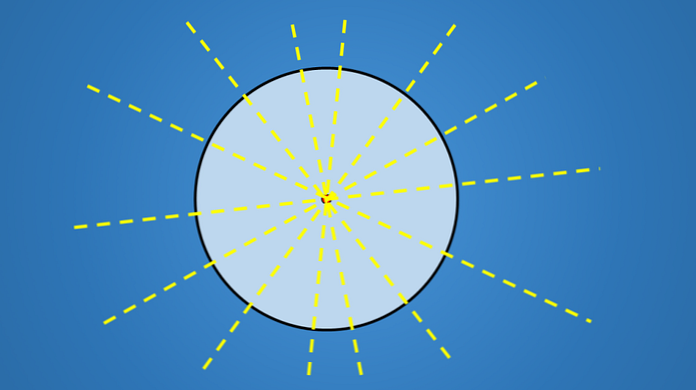
Jiné geometrické obrazce, takový jako trojúhelník, čtyřúhelník, pětúhelník, šestiúhelník nebo nějaký jiný polygon, mít konečný počet os symetrie.
Důvod proč kruh má nekonečný počet os symetrie je že to má žádné strany.
Odkazy
- Basto, J. R. (2014). Matematika 3: Základní analytická geometrie. Redakční skupina Patria.
- Billstein, R., Libeskind, S., & Lott, J. W. (2013). Matematika: přístup k řešení problémů učitelů základních škol. López Mateos Editori.
- Bult, B., & Hobbs, D. (2001). Matematický slovník (znázorněno na obr.). (F. P. Cadena, Trad.) Edice AKAL.
- Callejo, I., Aguilera, M., Martinez, L., & Aldea, C. (1986). Matematika Geometrie Reforma horního cyklu E.G.B. Ministerstvo školství.
- Schneider, W., & Sappert, D. (1990). Praktický technický nákres: úvod do základů průmyslového technického kreslení. Reverte.
- Thomas, G. B., & Weir, M. D. (2006). Výpočet: několik proměnných. Pearson Education.


